In this section, we will explore the concept of sphenic numbers and develop Java programs to determine whether a given number is sphenic or not. The identification of sphenic numbers is a common requirement in Java coding tests and academic assignments. Our focus will be on presenting the information without plagiarizing existing content while refraining from providing any extraneous details.
What is a Sphenic Number?
A sphenic number is a positive integer that meets two criteria. Firstly, it can be expressed as the product of three distinct prime numbers, denoted as p, q, and r. In other words, if a number n is sphenic, it can be written as n = p * q * r, where p, q, and r are prime numbers. Secondly, sphenic numbers have exactly 8 divisors. This sequence of numbers is identified as A007304 in the OEIS. To better grasp this concept, let’s consider an example.
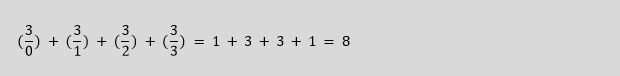
The eight divisors are as follows:
- 1
- Three distinct primes
- Three semi-primes (in which each of the distinct prime factors of the sphenic number is omitted)
- The sphenic number itself
Let’s consider the number 42 and check whether it is sphenic or not.
The factors of 42 are 1, 2, 3, 7, and 21. We will now identify the 8 divisors:
- 21 is a product of 3 and 7, with 2 omitted.
- 14 is a product of 2 and 7, with 3 omitted.
- 6 is a product of 2 and 3, with 7 omitted.
- 42 itself.
Therefore, we can conclude that 42 is indeed a sphenic number since it satisfies the conditions of having three distinct prime factors (2, 3, and 7), and their product yields the original number.
Note that sphenic numbers are not the only numbers with 8 divisors. Another category of numbers with 8 divisors includes those that result from the product of a prime number raised to the cube and another prime number, as well as those obtained by raising a prime number to the seventh power.
Sphenic Number Example
Let’s consider the number 30 to determine if it is a sphenic number.
The smallest three prime factors that, when multiplied together, yield the number 30 are 2, 3, and 5. Hence, the number 30 is indeed a sphenic number.
Now, let’s examine another number, 110.
The divisors of 110 are 1, 2, 5, 10, 11, 22, 55, and 110.
The smallest three prime factors that, when multiplied together, give the number 110 are 2, 5, and 11. Consequently, the number 110 qualifies as a sphenic number.
Let’s consider another number, 23.
The divisors of 23 are 1 and 23.
Since there are only two prime factors, namely 1 and 23, the number 23 does not meet the criteria for being a sphenic number.
Similarly, we can apply this process to other numbers as well. Some examples of sphenic numbers include 78, 102, 105, 110, 285, 286, 290, 310, 318, 322, and 345. For a comprehensive list of all sphenic numbers up to 10000, one can refer to the information provided by OEIS.
Sphenic Number Java Program
To determine if a number is a sphenic number, we can follow a two-step process. First, we need to verify if the number has exactly 8 divisors. After confirming this, we then proceed to check if the first three digits of the number (excluding 1) are prime.
SphenicNumberExample1.java
import java.util.*;
public class SphenicNumberExample
{
//create a global array of size 100000
static boolean arr[] = new boolean[10000];
//finds all the primes smaller than the limit
static void findPrime()
{
//marks all entries as true
//A value in mark[p] will finally be false if 'p' is Not a prime, else true.
Arrays.fill(arr, true);
//iterate over all the numbers so that their multiples can be marked as composite
for(int p = 2; p * p < 10000; p++)
{
//if p is not changed, then it is a prime
if(arr[p])
{
//update all the multiples of p
for(int i = p * 2; i < 10000; i = i + p)
arr[i] = false;
}
}
}
//user-defined function that checks if the given number is sphenic or not
static int isSphenic(int N)
{
//creating an array that stores the 8 divisors
int []arr1 = new int[8];
//counts the divisors
int count = 0;
int j = 0;
for(int i = 1; i <= N; i++)
{
if(N % i == 0 && count < 8)
{
//increments the count by 1
count++;
arr1[j++] = i;
}
}
//checks that there is exactly 8 divisors or not and all the numbers are distincit prime or not
//if yes returns 1, else returns 0
if(count == 8 && (arr[arr1[1]] && arr[arr1[2]] && arr[arr1[3]]))
return 1;
return 0;
}
//driver code
public static void main(String args[])
{
//calling user-defined function that find the priime numbers
findPrime();
Scanner sc=new Scanner(System.in);
System.out.print("Enter a number to check: ");
//reading an iteger from the user
int n=sc.nextInt();
int result = isSphenic(n);
if(result == 1)
//prints yes if the above condition returns true
System.out.print("Yes, the given number is sphenic.");
else
//prints no if the above condition returns false
System.out.print("No, the given number is not a sphenic.");
}
}
Output 1:
Enter a number to check: 165 Yes, the given number is sphenic.
Output 2:
Enter a number to check: 18967 No, the given number is not a sphenic.
SphenicNumberExample2.java
import java.util.*;
public class SphenicNumberExample1
{
public static void main(String args[])
{
Scanner sc=new Scanner(System.in);
int lower, upper, i, n, f, count, k;
System.out.print("Enter the lower limit: ");
//reads the lower limit from the user
lower=sc.nextInt();
System.out.print("Enter the upper limit: ");
//reads the upper limit from the user
upper=sc.nextInt();
System.out.println("\nSphenic numbers between the given range are: ");
for(i=lower;i<=upper;i++)
{
n=i;
k=0;
//defining an array that stores distinct prime factors
int prime[]={0,0,0};
//finds all the prime factors
for(f=2; n!=1;f++)
{
//counts the frequency of the prime factors
count=0;
while(n%f==0)
{
count++;
n=n/f;
}
if(count==1)
prime[k++]=f;
if(k==prime.length)
//breaks the execution if there are 3 unique prime factors
break;
}
//multiplying the prime factors
n=prime[0]*prime[1]*prime[2];
//compares the product (n) with the original number (i)
if(i==n)
System.out.print(i+" ");
}
System.out.println();
}
}
Output:
Enter the lower limit: 1 Enter the upper limit: 200 Sphenic numbers between the given range are: 30 42 66 70 78 102 105 110 114 130 138 154 165 170 174 182 186 190 195
SphenicNumberExample3.java
import java.util.*;
public class SphenicNumberExample2
{
public static void main(String args[])
{
Scanner sc=new Scanner(System.in);
int x,num,i,j,a,b,cp,ctr;
System.out.print("Enter the lower limit: ");
a=sc.nextInt();
System.out.print("Enter the upper limit: ");
b=sc.nextInt();
for(num=a;num<=b;num++)
{
int c=0, f=1;
cp=num;
ctr=0;
for (x=2;x<=cp;x++)
{
c=0;
while((cp%x)==0)
{
cp=cp/x;
c++;
}
if(c==1)
{
f=f*x;
ctr++;
}
}
if(f==num && ctr==3)
System.out.print(num+"\t");
}
}
}
Output:
Enter the lower limit: 1 Enter the upper limit: 100 30 42 66 70 78
To gain further knowledge on topics like Sphenic Number in Java, make sure to visit tutorials.freshersnow.com regularly.
