In this section, we will explore the concept of Keith numbers and develop Java programs to determine if a given number is a Keith number. Checking whether a number is a Keith number
What is Keith Number?
A positive number X with n digits is referred to as a Keith number or repfigit number. This classification arises from a unique number sequence that is generated using the digits of X. The sequence begins with the first n terms being the digits of X, while the subsequent terms are recursively calculated as the sum of the previous n terms. Examples of Keith numbers include 197, 19, 742, 1537, and so on.
Keith Number Example
Let’s determine if the number 742 is a Keith number or not.
First, we separate each digit of the number, which gives us 7, 4, and 2.
Next, we calculate the next term of the series by adding these digits together (7 + 4 + 2), resulting in 13.
The series now becomes 7, 4, 2, and 13.
To find the next term, we add the last three terms of the series (2 + 4 + 13), which gives us 19.
The series now becomes 7, 4, 2, 13, 19.
We continue this process, adding the last three terms each time, to generate the subsequent terms of the series.
Eventually, we reach the number 742 as a term of the series.
Since we have obtained the same number (742) as a term of the series, we can conclude that the given number, 742, is a Keith number.

By observing the previous example, we can note that to determine if a number is a Keith number, we need to calculate the terms of the series until we obtain the same number that we started with as a term of the series.
Let’s take another example.
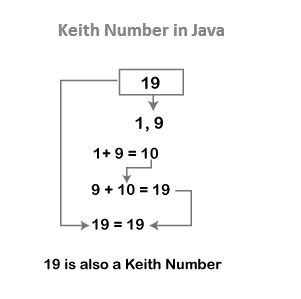
Steps to Find Keith Number
To check if a given number (X) is a Keith number, follow these steps:
- Read or initialize the number (X).
- Separate each digit from the given number (X).
- Add all the n-digits together to obtain the next term of the series.
- Add the last n terms of the series to find the next term.
- Repeat step 4 until we obtain a term that is the same as the original number we started with.
Keith Number Java Program
The logic behind identifying Keith numbers is relatively straightforward. We compute a series by adding the sum of the n previous numbers, where n is the number of digits in the input number. If, at any point, one of the computed numbers in the series matches the input number, it is considered a Keith number. The program terminates if the computed value exceeds the input number.
KeithNumberExample1.java
import java.util.*;
class KeithNumberExample
{
//user-defined function that checks if the given number is Keith or not
static boolean isKeith(int x)
{
//List stores all the digits of the X
ArrayList<Integer> terms=new ArrayList<Integer>();
//n denotes the number of digits
int temp = x, n = 0;
//executes until the condition becomes false
while (temp > 0)
{
//determines the last digit of the number and add it to the List
terms.add(temp%10);
//removes the last digit
temp = temp/10;
//increments the number of digits (n) by 1
n++;
}
//reverse the List
Collections.reverse(terms);
int next_term = 0, i = n;
//finds next term for the series
//loop executes until the condition returns true
while (next_term < x)
{
next_term = 0;
//next term is the sum of previous n terms (it depends on number of digits the number has)
for (int j=1; j<=n; j++)
next_term = next_term + terms.get(i-j);
terms.add(next_term);
i++;
}
//when the control comes out of the while loop, there will be two conditions:
//either next_term will be equal to x or greater than x
//if equal, the given number is Keith, else not
return (next_term == x);
}
//driver code
public static void main(String[] args)
{
//calling the user-defined method inside the if statement and print the result accordingly
if (isKeith(19))
System.out.println("Yes, the given number is a Keith number.");
else
System.out.println("No, the given number is not a Keith number.");
if(isKeith(742))
System.out.println("Yes, the given number is a Keith number.");
else
System.out.println("No, the given number is not a Keith number.");
if(isKeith(4578))
System.out.println("Yes, the given number is a Keith number.");
else
System.out.println("No, the given number is not a Keith number.");
}
}
Output:
Yes, the given number is a Keith number. Yes, the given number is a Keith number. No, the given number is not a Keith number.
We will now develop a Java program to discover all the Keith numbers that have the same number of digits.
KeithNumberExample2.java
import java.util.Scanner;
public class KeithNumberExample1
{
public static void main(String args[])
{
Scanner sc= new Scanner(System.in);
System.out.print("Enter the number of digits the series must have: ");
//reads an integer as length of the number from the user
int numlen = sc.nextInt();
//checks if the length of the number is greater than 2 or not
if (numlen < 2)
{
//prints if the above condition returns false
System.out.println("The number must have at least 2 digits.");
}
//executes if the above condition returns true
else
{
//calculates the lower bound from where the series starts
long lowBound = (long) Math.pow(10, numlen - 1);
//calculates the upper bound from where the series ends
long upperBound = (long) Math.pow(10, numlen);
for (long l = lowBound; l < upperBound; l++)
{
if (isKeith(String.valueOf(l)))
{
//prints all the Keith number between given range
System.out.print(l + ", ");
}
}
}
sc.close();
}
//function that checks whether the given number is Keith or not
public static boolean isKeith(String input)
{
int numlen = input.length();
//keep track only the last three terms
long[] series = new long[numlen];
for (int i = 0; i < numlen; i++)
{
series[i] = Long.valueOf(input.substring(i, i + 1));
}
long next_term = 0;
long number = Long.valueOf(input);
while (next_term < number)
{
next_term = 0;
//calculates next term of the series
for (int i = 0; i < numlen; i++)
{
next_term = next_term + series[i];
if (i < numlen - 1)
{
//shift series to the left
series[i] = series[i + 1];
}
else
{
//add new value to the series
series[i] = next_term;
}
}
//compares the next term of the series with the number and returns boolean value accordingly
if (next_term == number)
{
return true;
}
}
return false;
}
}
Output 1:
Enter the number of digits the series must have: 5 31331, 34285, 34348, 55604, 62662, 86935, 93993,
Output 2:
Enter the number of digits the series must have: 2 14, 19, 28, 47, 61, 75,
In a similar manner, we can identify Keith numbers with d digits. The table below provides a summary of d-digit Keith numbers.
| d | d-digit Keith Numbers |
|---|---|
| 2 | 14, 19, 28, 47, 61, 75 |
| 3 | 197, 742 |
| 4 | 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909 |
| 5 | 31331, 34285, 34348, 55604, 62662, 86935, 93993 |
| 6 | 120284, 129106, 147640, 156146, 174680, 183186, 298320, 355419, 694280, 925993 |
| 7 | 1084051, 7913837 |
| 8 | 11436171, 33445755, 44121607 |
| 9 | 129572008, 251133297 |
| 10 | (none) |
| 11 | 24769286411, 96189170155 |
| 12 | 171570159070, 202366307758, 239143607789, 296658839738 |
| 13 | 1934197506555, 8756963649152 |
| 14 | 43520999798747, 74596893730427, 97295849958669 |
| 15 | 120984833091531, 270585509032586, 754788753590897 |
| 16 | 3621344088074041, 3756915124022254, 4362827422508274 |
| 17 | 11812665388886672, 14508137312404344, 16402582054271374, 69953250322018194, 73583709853303061 |
| 18 | 119115440241433462, 166308721919462318, 301273478581322148 |
| 19 | 1362353777290081176, 3389041747878384662, 5710594497265802190, 5776750370944624064, 6195637556095764016 |
| 20 | 12763314479461384279, 27847652577905793413, 45419266414495601903 |
| 21 | 855191324330802397989 |
| 22 | 7657230882259548723593 |
| 23 | 26842994422637112523337, 36899277593852609997403, 61333853602129819189668 |
| 24 | 229146413136585558461227 |
| 25 | 9838678687915198599200604 |
To discover more insights about Keith Numbers in Java, make sure to follow tutorials.freshersnow.com.
