In this section, we have explored various approaches in Java programs to determine the Greatest Common Divisor (GCD) of two numbers.
The GCD represents the highest number that divides two or more numbers without leaving any remainder. It is commonly abbreviated as GCD and is also referred to as the Greatest Common Factor (GCF) or the Highest Common Factor (HCF). The GCD is frequently employed in simplifying fractions and solving mathematical problems.
How to Find the Greatest Common Factor
- Write all the factors of each number.
- Select the common factors.
- Select the greatest number, as GCF.
Example: To find the Greatest Common Factor (GCF) of two numbers, 14 and 9, we can use the following approach:
Factors of 14: 1, 2, 7, 14
Factors of 9: 1, 3, 9
Common factors: 1
GCF of 14 and 9: 1
Therefore, the GCF of 14 and 9 is 1.
Algorithm to Find GCD
- Declare two variables x, and y, to represent the two numbers for which you want to find the GCD.
- Set up a loop that iterates from 1 to the maximum of x and y.
- Within the loop, check if the current number divides both x and y without leaving any remainder. If it does, store the number in a variable.
- After the loop completes, the stored number will be the GCD of x and y.
In Java, we can use the following ways to find the GCD of two numbers:
- Using Java for loop
- Using while loop
- Using User-Defined Method
- Using the Euclidean Algorithm
- Using Modulo Operator
Using Java for loop
In the given program, we have initialized two numbers, x and y, with the values 12 and 8 respectively. A for loop has been utilized, which iterates from 1 to the smallest of the two numbers. The loop continues executing as long as the condition i <= x && i <= y evaluates to true. Inside the loop, an if statement checks the condition (x % i == 0 && y % i == 0) and returns true if both conditions are satisfied. If the condition is true, the value of i is stored in the variable gcd. Finally, the program prints the value of the gcd variable.
FindGCDExample1.java
public class FindGCDExample
{
public static void main(String[] args)
{
//x and y are the numbers to find the GCF
int x = 12, y = 8, gcd = 1;
//running loop form 1 to the smallest of both numbers
for(int i = 1; i <= x && i <= y; i++)
{
//returns true if both conditions are satisfied
if(x%i==0 && y%i==0)
//storing the variable i in the variable gcd
gcd = i;
}
//prints the gcd
System.out.printf("GCD of %d and %d is: %d", x, y, gcd);
}
}
Output:
GCD of 12 and 8 is: 4
Using Java while Loop
In the provided example, a while loop has been employed to test the condition n1 != n2. The loop continues executing as long as the condition evaluates to true, indicating that n1 is not equal to n2.
FindGCDExample1.java
public class FindGCDExample1
{
public static void main(String[] args)
{
int n1=50, n2=60;
while(n1!=n2)
{
if(n1>n2)
n1=n1-n2;
else
n2=n2-n1;
}
System.out.printf("GCD of n1 and n2 is: " +n2);
}
}
Output:
GCD of n1 and n2 is: 10
FindGCDExample2.java
public class FindGCDExample2
{
public static void main(String[] args)
{
int Num1=12, Num2=8, Temp, GCD=0;
while(Num2 != 0)
{
Temp = Num2;
Num2 = Num1 % Num2;
Num1 = Temp;
}
GCD = Num1;
System.out.println("\n GCD = " + GCD);
}
}
Output:
GCD = 4
Using User-Defined Method
The provided program includes a method called findGCD(), which is responsible for calculating the Greatest Common Divisor (GCD) of two numbers. The method takes two integer parameters, a and b.
FindGCDExample3.java
import java.util.Scanner;
public class FindGCDExample3
{
//private static Scanner sc;
public static void main(String[] args)
{
int a, b, gcd = 0;
Scanner sc = new Scanner(System.in);
System.out.print("Enter the First Number: ");
a = sc.nextInt();
System.out.print("Enter the Second Number: ");
b = sc.nextInt();
gcd = findGCD(a, b);
System.out.println("GCD of " + a + " and " + b + " = " + gcd);
}
public static int findGCD(int a, int b)
{
while(b != 0)
{
if(a > b)
{
a = a - b;
}
else
{
b = b - a;
}
}
return a;
}
}
Output:
Enter the First Number: 75 Enter the Second Number: 125 GCD of 75 and 125 = 25
Using the Euclidean Algorithm
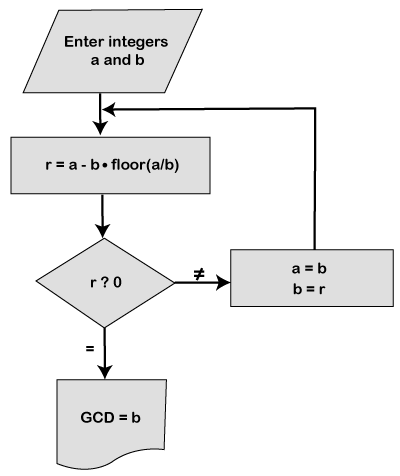
The Euclidean Algorithm, also known as Euclid’s Algorithm, is a highly efficient method for calculating the Greatest Common Divisor (GCD) of two numbers. The algorithm follows the following principles:
- If A is equal to 0, then the GCD(A, B) is equal to B since the GCD of 0 and B is B. At this point, the algorithm can be terminated.
- If B is equal to 0, then the GCD(A, B) is equal to A since the GCD of A and 0 is A. At this point, the algorithm can be terminated.
- Write A in terms of the quotient obtained from the division (A = B * Q + R).
FindGCDExample4.java
import java.util.Scanner;
public class FindGCDExample4
{
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
System.out.println("Enter the two numbers: ");
int x = sc.nextInt();
int y = sc.nextInt();
System.out.println("The GCD of two numbers is: " + findGCD(x,y));
}
static int findGCD(int x, int y)
{
int r=0, a, b;
a = (x > y) ? x : y; // a is greater number
b = (x < y) ? x : y; // b is smaller number
r = b;
while(a % b != 0)
{
r = a % b;
a = b;
b = r;
}
return r;
}
}
Output:
Enter the two numbers: 11 33 The GCD of two numbers is: 11
Using Modulo Operator
The provided program includes a recursive function called findGCD(), which takes two integer parameters, a and b.
Within the findGCD() function, a conditional check is performed to determine if the second number (b) is equal to 0. If this condition is true, the function returns the value of a as the Greatest Common Divisor (GCD). Otherwise, if b is not equal to 0, the function recursively calls itself with the parameters a and a%b, effectively reducing the problem to a smaller instance.
FindGCDExample5.java
public class FindGCDExample5
{
public static void main(String[] args)
{
int a = 112, b = 543;
System.out.println("GCD of " + a +" and " + b + " is " + findGCD(a, b));
}
//recursive function to return gcd of a and b
static int findGCD(int a, int b)
{
if (b == 0)
return a;
return findGCD(b, a % b);
}
}
Output:
GCD of 112 and 543 is 1
FindGCDExample6.java
public class FindGCDExample6
{
public static void main(String[] args)
{
int a = 54, b = 24;
System.out.println("GCD of " + a +" and " + b + " is " + gcd(a, b));
}
//recursive function to return gcd of a and b
static int gcd(int a, int b)
{
// Everything divides 0
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return gcd(a-b, b);
return gcd(a, b-a);
}
}
Output:
GCD of 54 and 24 is 6
For additional learning resources, such as the Java program to find the GCD of two numbers, consider following tutorials.freshersnow.com.
