Java Program to Display the Upper Triangular Matrix

An upper triangular matrix is a special type of square matrix where all the elements below the principal diagonal are zero. To obtain the upper triangular matrix, the matrix must be square, meaning it has an equal number of rows and columns. The dimensions of a square matrix are conventionally represented as n x n.

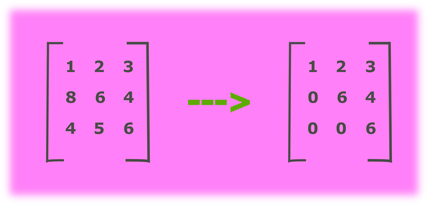
To convert a given matrix into an upper triangular matrix, it is necessary to loop through the matrix and set the values of the elements to zero where the row number is greater than the column number. In the provided example, the principal diagonal elements of the matrix are located at positions (1, 1), (2, 2), and (3, 3), with values (1, 6, 6) respectively. All the elements below the diagonal, such as (2, 1), (3, 1), and (3, 2), need to be set to zero.

Algorithm for a Java Program to Display the Upper Triangular Matrix

• • STEP 1: START
  • STEP 2: DEFINE rows, cols
  • STEP 3: INITIALIZE matrix a[][] ={{1,2,3},{8, 6, 4}, {4, 5, 6}}
  • STEP 4: rows = a.length
  • STEP 5: cols = a[0].length
  • STEP 6: if(rows!=cols)
    then
    PRINT “Matrix should be a square matrix”
    else
    Go to step 7
  • STEP 7: REPEAT STEP 8 to STEP 10 UNTIL i<rows
    //for(i=0; i<rows; i++)
  • STEP 8: REPEAT STEP 9 UNTIL j<cols // for(j=0; j<cols; j++)
  • STEP 9: If(i>j) then PRINT 0 else PRINT a[i][j]
  • STEP 10: PRINT new line
  • STEP 11: END

Java Program to Display the Upper Triangular Matrix

public class UpperTriangular    
{    
    public static void main(String[] args) {    
        int rows, cols;    
            
        //Initialize matrix a    
        int a[][] = {       
                        {1, 2, 3},    
                        {8, 6, 4},    
                        {4, 5, 6}    
                    };    
              
          //Calculates number of rows and columns present in given matrix    
          rows = a.length;    
        cols = a[0].length;    
            
        if(rows != cols){    
            System.out.println("Matrix should be a square matrix");    
        }    
        else {    
            //Performs required operation to convert given matrix into upper triangular matrix    
            System.out.println("Upper triangular matrix: ");    
            for(int i = 0; i < rows; i++){    
                for(int j = 0; j < cols; j++){    
                  if(i > j)    
                    System.out.print("0 ");    
                  else    
                    System.out.print(a[i][j] + " ");    
                }    
                System.out.println();    
            }    
        }    
    }    
}

Output:

Upper triangular matrix:
1    2   3
0    6   4
0    0   0

n conclusion, the Java program to display the upper triangular matrix involves iterating through the matrix and setting the elements below the principal diagonal to zero. By comparing the row number to the column number, we can identify and modify the appropriate elements. Follow tutorials.freshersnow.com to learn more.